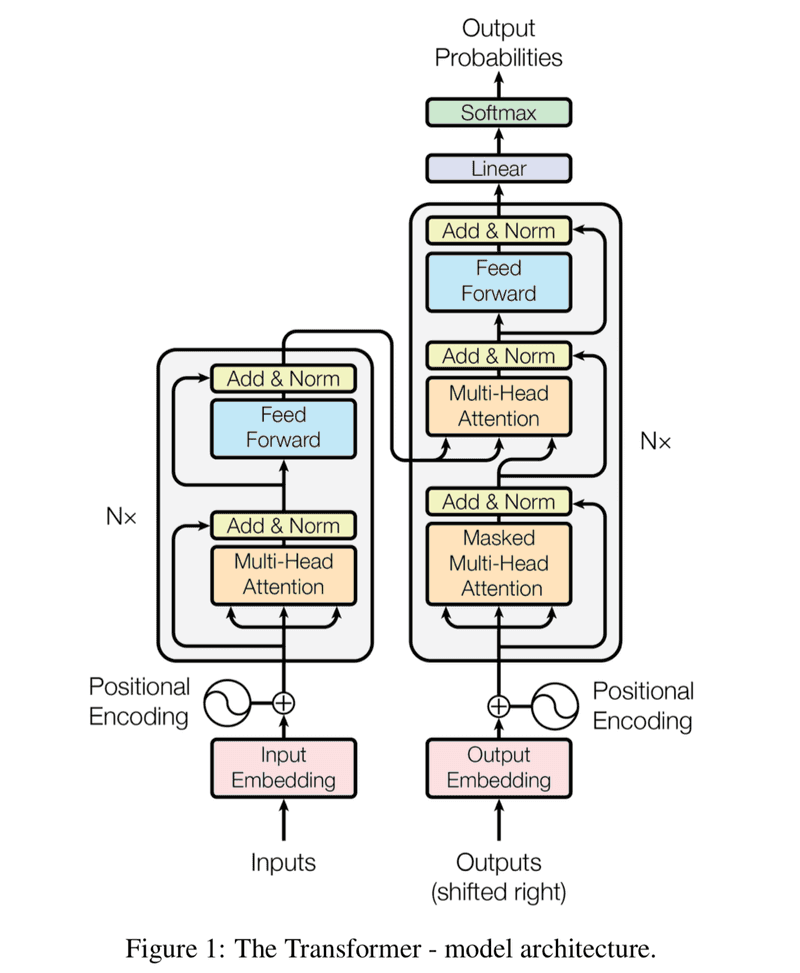
Transformers are revolutionising AI - but how do they work? The 2017 paper that introduces them (entitled "Attention is All You Need") includes Figure 1, which is a diagram of the transformer architecture. This diagram is not particularly comprehensible unless you understand the building blocks. I'll briefly explain these building blocks in this blog post. For an in depth discussion please refer to the original paper.
Transformers can be used for applications such as language translation and personal assistants. The reason they're so effective at dealing with natural language tasks is that they're good at representing natural language inputs as vectors, where the vectors represent both the meaning of the individual words, and, most importantly, the contextual relationships between them.
Multi-head Attention
As we shall see, the only complicated component in the above architecture is the multi-head attention block, so we'll begin with this.
Imagine that we have an input comprising 4 english words such as: "The cat got fat". First we find the word embedding for each of the 4 terms. Let's call these v1 v2 v3 v4
Note: A word embedding is a representation of a word, as a vector, such that related words are represented closely together in the vector space.
We then calculate scores for each term. The scores for the third term, for example, are calculated by finding the dot products as follows:
s31 = v3 ⋅ v1
s32 = v3 ⋅ v2
s33 = v3 ⋅ v3
s34 = v3 ⋅ v4
We do this for each of the 4 terms, not just term 3 or course. Note that if v3 = [a b c] and v1 = [d e f], then v3 ⋅ v1 = v31 = ad + be + cf.
We then normalise the scores, which means, in the case of the third term for example, that we make the values s31 s32 s33 & s34 add to 1.
The normalised scores (aka weights) are named: w31 w32 w33 w34.
Putting it mathematically:
Σjw1j = 1
Σjw2j = 1
Σjw3j = 1
Σjw4j = 1
We then multiply the weights by the input vectors to get new vectors:
y1 = v1w11 + v2w12 + v3w13 + v4w14
y2 = v1w21 + v2w22 + v3w23 + v4w24
y3 = v1w31 + v2w32 + v3w33 + v4w34
y4 = v1w41 + v2w42 + v3w43 + v4w44
These new vectors are more useful than the original word embeddings because they include context based on the relationships between each word.
You may have noticed that there's been no training, in the ML sense of the word, so far. We need the system to be trainable, so we add a few matrices to turn it into a neural network. The matrices are effectively linear layers.
The naming of the matrices is based on an analogy with databases. You can make your own mind up if this analogy is a good one or not, but the idea is that we have a key, a query, and a value.
The input vectors get multiplied by the key matrix.
The vectors at the dot product step get multiplied by the query matrix.
The input vectors at the normalised score (weight) multiplying step get multiplied by the value matrix.
We now add named entity recognition (NER) and train with traditional backpropagation.
We also add scaling to avoid saturating the softmax function.
The resulting scaled dot product attention layer is known as a self attention block.
Now we parallelise multiple self attention blocks, where each replica is known as a "head". There is no sharing of weights between these heads. The idea is that each head attends to information from different representation subspaces at different positions.
We now add masking so that each word can only attend to the words that come before it, and finally concatenate the outputs and pass through a dense layer. The result is called a multi-head attention block. If you recall, the multi-head attention block is the component that I said was the only difficult thing to understand in Figure 1.
Speaking of the transformer in Figure 1, the input is not just 4 words, but a batch of sentences, where each word is encoded into a 512 dimensional representation.
The output, after training, should be a set of vectors that represent the meaning of the sentences.
The Rest of the Transformer
You'll notice in figure one that the outputs of the multi-head attention blocks are added to the inputs and normalised. This is to avoid the vanishing gradients problem during training.
Multi-head attention blocks don't factor in the order of the words. The word order is only one of the things that brings meaning to a sentence (or paragraph etc), but it's nevertheless vital. The positional encoder, illustrated in Figure 1, adds in the positional information. There are many ways to implement this, but suffice is to say that you can either train it using the gradient signal, or use some kind of principled function, such as sine and cosine functions of different frequencies as was done in the original paper.
The other thing to note is that the encoders themselves can be stacked (i.e. parallelised). Figure 1 indicates this with the Nx notation, where N happened to be 6 in the case of the original paper.
We can then just add more blocks as desired.
And that's all there is to it. It looks like a bit of an unwieldy architecture at first blush, but it works well, and it's highly scalable.